I’ve been learning at least one new programming language per month through Exercism and the #12in23 challenge. I’ve keep saying, every time you learn a new language, you learn something about all the others you know. Plus, once you know \(N\) languages, the \(N+1^{\rm th}\) is significantly easier. This post covers a calculation I came across in Haskell, and how I can now do the same in a lot of other languages - and perhaps can’t as easily in others.
All of the languages here, I’m learning via Exercism, or at least I’m completing a handful or more exercises in each of the languages, which means learning enough of the syntax to be able to complete those. The #12in23 challenge is to try 12 languages in 2023… I’m doing just fine so far
Haskell
I’ve been reading the (great!) online version of Learn You a Haskell for Great Good! - Haskell is a (properly) “pure” functional language, part of which means it has no side-effects, which includes, say, printing to the console. Haskell, of course, has a way around this (monads!) but it means there’s a lot to get through before you even get to a printing “Hello, World!” example. It’s also lazy which means it doesn’t evaluate something if it doesn’t need to, which makes for some good performance, sometimes.
This video does a really nice job explaining the principles of pure functional programming using JavaScript to introduce Haskell, building recursive functions that only take a single argument and return a single value.
One example that caught my eye in the list comprehensions section was this
ghci> let rightTriangles' = [ (a,b,c) | c <- [1..10], b <- [1..c], a <- [1..b], a^2 + b^2 == c^2, a+b+c == 24]
ghci> rightTriangles'
[(6,8,10)] This perhaps isn’t too hard to read, even for those unfamiliar with the language. ghci is
the interactive REPL for the Glasgow Haskell Compiler, so the prompt starts with that.
Haskell uses a let binding to identify variables, and the apostrophe just indicates that
this is a slightly different version compared to the one defined slightly earlier in the chapter.
The list comprehension itself is perhaps not so dissimilar to one you’d find in Python; it
defines some tuple (a, b, c) and | identifies some constraints, namely that c is taken
from a range of 1 to 10, b is taken from a range of 1 to c, and a is taken from
a range of 1 to b, along with the criteria that \(a^2 + b^2 = c^2\) (the numbers form a Pythagorean
triple) and their sum is 24. I discussed the Pythagorean triples in my last post - no
coincidence (/s). If you evaluate this line, you more-or-less immediately get back the result
[(6,8,10)]which is a Pythagorean triple
\[6^2 + 8^2 = 36 + 64 = 100 = 10^2\]
for which
\[a + b + c = 6 + 8 + 10 = 24\] This isn’t a groundbreaking calculation, but I’ve done a lot of R, and my mind was a little blown that such a calculation could really be done in a single line just by specifying those constraints. Not a solver, not a grid of values with a filter, just specifying constraints.
R
Anyone who knows me knows I write a lot of R. I wrote a book on it. I solved all of the Advent of Code 2022 puzzles in strictly base R (I really need to write that post).
Now, R (unfortunately) doesn’t have any comprehensions, list or otherwise, so I started to wonder how I would do this in R. The best I can come up with is
expand.grid(a=1:10, b=1:10, c=1:10) |>
dplyr::filter(a^2 + b^2 == c^2 &
a + b + c == 24 &
a < b &
b < c)## a b c
## 1 6 8 10but that involves explicitly creating all 1000 combinations of a, b, and c. There
may be a multi-step way to limit the grid to \(a < b\) and \(b < c\) but that’s more code. Maybe the
Haskell solution also has to generate these behind the scenes, but it isn’t up to the user to
do that, so it feels nicer. I like the filter() verb here - technically the & joining is
redundant and I could have passed each condition as its own argument. expand.grid() is one
of those underutilised functions that comes in very handy sometimes - or its cousin
tidyr::crossing() which wraps this and additionally performs de-duplication and sorting.
Now that I know more languages, I felt I could explore this a bit further!
Python
In Python, which I feel is well-known for list comprehensions, this translates more or less 1:1 to
[(a,b,c) for c in range(1,11) for b in range(1,c) for a in range(1,b) if ((a**2 + b**2) == c**2) if a+b+c==24][(6, 8, 10)]Of course, ranges are specified differently, but otherwise this follows the Haskell
solution quite nicely, including the dynamic ranges of b and a which avoids needing
to search the entire 10*10*10 space.
I appreciate there’s a silly language war between Python and R but honestly, a lot of stuff is written in Python and a lot of people write in Python. I figure it’s better to understand that language for when I need it than to stick my head in the sand and claim some sort of superiority. There’s bits I don’t like, sure, but that doesn’t mean I shouldn’t learn it. I’m even registered and attending PyConAU next weekend.
Rust
Rust is a fun language with easily the most helpful compiler ever made - you can make a lot of mistakes, but the error messages and hints are unparalleled. I’m currently taking Tim McNamara’s ‘How To Learn Rust’ course which has a lot of practical lessons and I’ve built some fun things already. I completed the first 13 Advent of Code 2022 puzzles in Rust, after which it all got a bit too complicated (and I do really need to write that post).
Rust doesn’t have list comprehensions (I believe there are cargo crates which do add such functionality) so it’s back to nested loops
for c in 1..=10 {
for b in 1..=c {
for a in 1..=b {
if a*a + b*b == c*c && a+b+c == 24 {
println!("{}, {}, {}", a, b, c);
}
}
}
};6, 8, 10That doesn’t allocate a result at all, it just prints the values when it encounters them, and since the loop is nested, it can limit the search to \(b \leq c\) and \(a \leq b\), but it does explicitly run the loop across all those combinations. It’s possible there’s a much better way to do this, but I couldn’t think of it.
Common Lisp
I like the idea of Common Lisp, and I’m making my way through Practical Common Lisp slowly. I suspect I enjoy some of the descendants like Clojure a bit more, but it’s absolutely worth learning. Miles McBain has a great post about how learning about lisp quoting helps understand more of the tidyverse. I have used lisp in a code-golf post.
Lisp doesn’t have comprehensions so it relies on loops, and again, just prints the
result, returning NIL
(loop for c from 1 to 10
do (loop for b from 1 to c
do (loop for a from 1 to b
do (when (and (= (+ a b c) 24) (= (+ (* a a) (* b b)) (* c c)))
(format t "~d, ~d, ~d~%" a b c)))))
6, 8, 10
NILThe loop is still constrained to \(b \leq c\) and \(a \leq b\), but definitely runs through all those values.
Julia
I really want to learn more Julia, but I’m not entirely new to the language. I have completed the first 25 Project Euler problems in Julia (by no means optimised solutions). I think what’s holding me back is the fact that almost every presentation using it is so very mathsy - and I’m a physicist by training. I love that the tidyverse is making its way over in the forms of Queryverse, DataFramesMeta, and more recently (and most likely with more success) the Tidier family.
Julia does have list comprehensions, and additionally has an “element” operator with
the mathematically-familiar symbol ∈
[(a,b,c) for c ∈ 1:10, b ∈ 1:10, a ∈ 1:10 if (a^2 + b^2 == c^2) && (a+b+c == 24) && b <= c && a <= b]1-element Vector{Tuple{Int64, Int64, Int64}}:
(6, 8, 10)Unfortunately, the choices for b and a still need to run through all 10 values because
Julia doesn’t allow these to be co-defined like Haskell and Python do. I came to Julia from
mainly only knowing R, so dealing with an output of type Vector{Tuple{Int64, Int64, Int64}}
initially proved to be a challenge, but I’d say learning more Rust has made me feel a lot more
comfortable around working with types.
Clojure
Clojure feels to me like “lisp, but with good libraries”. There’s definitely syntax differences, but most of them feel like improvements.
(for [c (range 11)
b (range c)
a (range b)
:when (and (== (+ (* a a) (* b b)) (* c c)) (== (+ a b c) 24))]
[a b c])([6 8 10])This still feels like a comprehension, but the syntax is certainly a bit more
convoluted. Bonus points for the dynamic ranges of b and a. Still, a long way
off of completely unreadable, I’d say.
Scala
I’m learning a lot of functional programming, and I think I’m happy that some of the textbooks use Scala rather than some alternatives. I’m still very new to this language, but so far I think I like it.
Again, we’re back to a loop, but most of it is straightforward assignments and we
get the dynamic ranges of b and a
for {
c <- 1 until 11
b <- 1 until c
a <- 1 until b
if a * a + b * b == c * c & a + b + c == 24
} {
println(s"Side lengths: $a, $b, $c")
}Side lengths: 6, 8, 10C
I mentioned that I performed this calculation in C in my last post - that ends up being just a loop
int a, b, c
printf("%4s\t%4s\t%4s\t%4s\n", "a", "b", "c");
printf(" -------------------------\n");
for (c = 1; c <= 24; c++)
for (b = 1; b <= c; b++)
for (a = 1; a <= b; a++)
if ( ( pow ( a, 2 ) + pow ( b, 2 ) ) == pow ( c, 2 ) ) {
printf("%4i\t%4i\t%4i\t%4i\n", a, b, c);
}I haven’t run the output directly, since it needs an entire program supporting it, but it’s the right answer.
So, what does it look like if you run all of these together? I’ve been getting back into using tmux and it’s very powerful. One of the features is splitting a window into panes, so I did that - one for each of these languages!
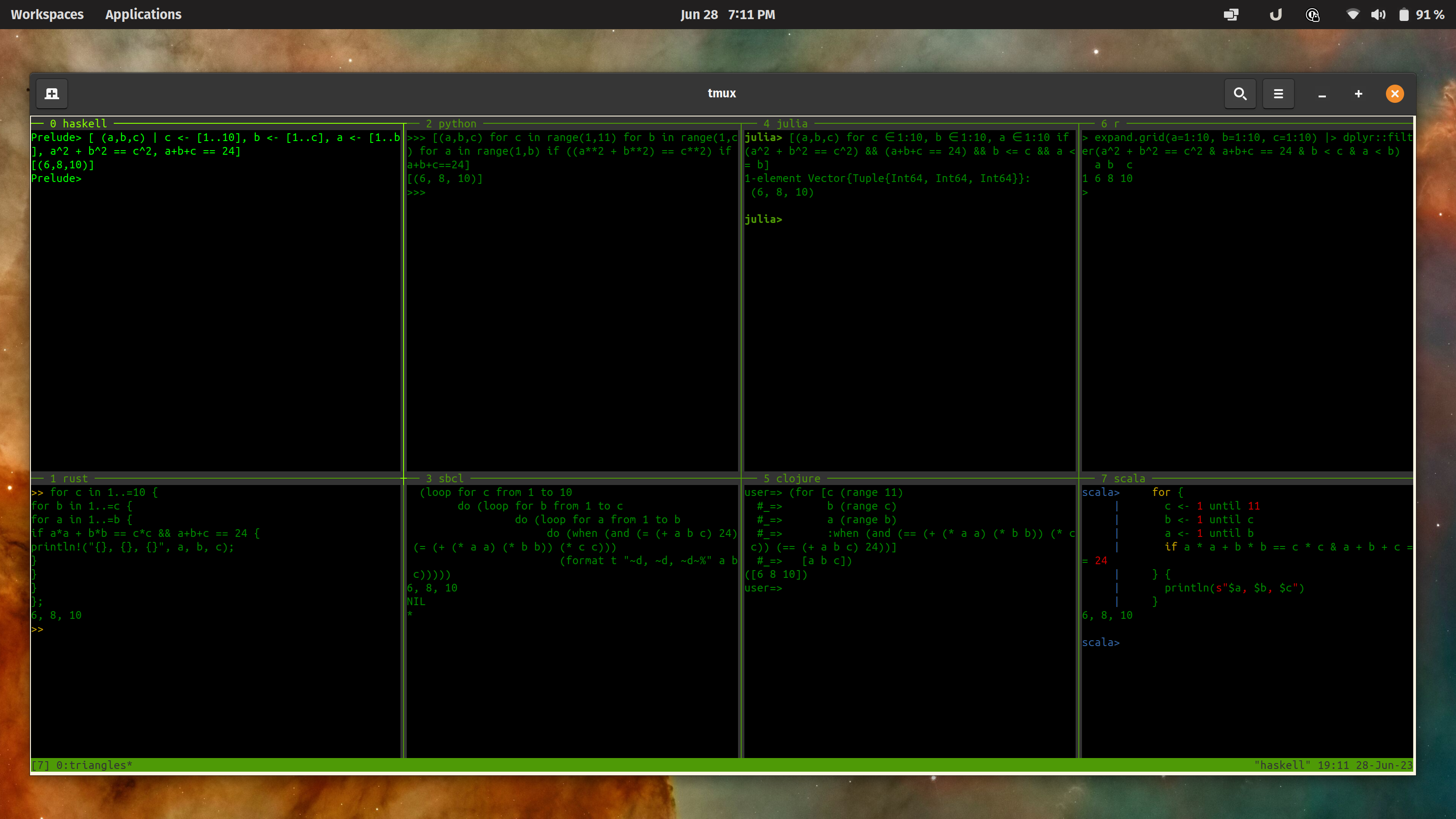
I still think the Haskell solution shines above all the rest. It has all of the simplicity and language richness with none of the boilerplate. I like that it’s declarative (“get an answer to this”) rather than imperative (“do this, then that, then loop here…”). Comparing all of these, it’s clear there’s no guarantees about being able to define the dynamic iteration ranges so another win for Haskell, there.
Following my last post, @Kazinator mentioned to me that the “TXR Lisp code, calling calcsum directly via FFI using Lisp nested arrays” could be written as
$ cat calcsum.tl
(typedef arr3d (ptr (array (ptr (array (ptr (array int)))))))
(with-dyn-lib "./calcsum.so"
(deffi calcsum "calcsum" void (int (ptr arr3d))))
(let* ((dim 16)
(arr (vector dim)))
(each ((a 0..dim))
(set [arr a] (vector dim))
(each ((b 0..dim))
(set [[arr a] b] (vector dim 0))))
(calcsum (pred dim) arr)
(each-prod ((a 1..dim)
(b 1..dim)
(c 1..dim))
(let ((sum [[[arr a] b] c]))
(if (plusp sum)
(put-line (pic "### + ### + ### = ####" a b c sum))))))
$ txr calcsum.tl 3 + 4 + 5 = 12
5 + 12 + 13 = 30
6 + 8 + 10 = 24
9 + 12 + 15 = 36This calculates all the combinations up to some value (as my post did) but it’s already clear there’s some cool features there.
How does your favourite language calculate the Pythagorean triple with a sum of 24? What can I do better in the solution I have above for a language you know? I can be found on Mastodon or use the comments below.
devtools::session_info()
## ─ Session info ───────────────────────────────────────────────────────────────
## setting value
## version R version 4.1.2 (2021-11-01)
## os Pop!_OS 22.04 LTS
## system x86_64, linux-gnu
## ui X11
## language (EN)
## collate en_AU.UTF-8
## ctype en_AU.UTF-8
## tz Australia/Adelaide
## date 2023-08-13
## pandoc 3.1.1 @ /usr/lib/rstudio/resources/app/bin/quarto/bin/tools/ (via rmarkdown)
##
## ─ Packages ───────────────────────────────────────────────────────────────────
## package * version date (UTC) lib source
## blogdown 1.17 2023-05-16 [1] CRAN (R 4.1.2)
## bookdown 0.29 2022-09-12 [1] CRAN (R 4.1.2)
## bslib 0.5.0 2023-06-09 [3] CRAN (R 4.3.1)
## cachem 1.0.8 2023-05-01 [3] CRAN (R 4.3.0)
## callr 3.7.3 2022-11-02 [3] CRAN (R 4.2.2)
## cli 3.6.1 2023-03-23 [3] CRAN (R 4.2.3)
## crayon 1.5.2 2022-09-29 [3] CRAN (R 4.2.1)
## devtools 2.4.5 2022-10-11 [1] CRAN (R 4.1.2)
## digest 0.6.33 2023-07-07 [3] CRAN (R 4.3.1)
## dplyr 1.1.2 2023-04-20 [3] CRAN (R 4.3.0)
## ellipsis 0.3.2 2021-04-29 [3] CRAN (R 4.1.1)
## evaluate 0.21 2023-05-05 [3] CRAN (R 4.3.0)
## fansi 1.0.4 2023-01-22 [3] CRAN (R 4.2.2)
## fastmap 1.1.1 2023-02-24 [3] CRAN (R 4.2.2)
## fs 1.6.3 2023-07-20 [3] CRAN (R 4.3.1)
## generics 0.1.3 2022-07-05 [3] CRAN (R 4.2.1)
## glue 1.6.2 2022-02-24 [3] CRAN (R 4.2.0)
## htmltools 0.5.5 2023-03-23 [3] CRAN (R 4.2.3)
## htmlwidgets 1.5.4 2021-09-08 [1] CRAN (R 4.1.2)
## httpuv 1.6.6 2022-09-08 [1] CRAN (R 4.1.2)
## jquerylib 0.1.4 2021-04-26 [3] CRAN (R 4.1.2)
## jsonlite 1.8.7 2023-06-29 [3] CRAN (R 4.3.1)
## JuliaCall 0.17.5 2022-09-08 [1] CRAN (R 4.1.2)
## knitr 1.43 2023-05-25 [3] CRAN (R 4.3.0)
## later 1.3.0 2021-08-18 [1] CRAN (R 4.1.2)
## lattice 0.21-8 2023-04-05 [4] CRAN (R 4.3.0)
## lifecycle 1.0.3 2022-10-07 [3] CRAN (R 4.2.1)
## magrittr 2.0.3 2022-03-30 [3] CRAN (R 4.2.0)
## Matrix 1.6-0 2023-07-08 [4] CRAN (R 4.3.1)
## memoise 2.0.1 2021-11-26 [3] CRAN (R 4.2.0)
## mime 0.12 2021-09-28 [3] CRAN (R 4.2.0)
## miniUI 0.1.1.1 2018-05-18 [1] CRAN (R 4.1.2)
## pillar 1.9.0 2023-03-22 [3] CRAN (R 4.2.3)
## pkgbuild 1.4.0 2022-11-27 [1] CRAN (R 4.1.2)
## pkgconfig 2.0.3 2019-09-22 [3] CRAN (R 4.0.1)
## pkgload 1.3.0 2022-06-27 [1] CRAN (R 4.1.2)
## png 0.1-7 2013-12-03 [1] CRAN (R 4.1.2)
## prettyunits 1.1.1 2020-01-24 [3] CRAN (R 4.0.1)
## processx 3.8.2 2023-06-30 [3] CRAN (R 4.3.1)
## profvis 0.3.7 2020-11-02 [1] CRAN (R 4.1.2)
## promises 1.2.0.1 2021-02-11 [1] CRAN (R 4.1.2)
## ps 1.7.5 2023-04-18 [3] CRAN (R 4.3.0)
## purrr 1.0.1 2023-01-10 [1] CRAN (R 4.1.2)
## R6 2.5.1 2021-08-19 [3] CRAN (R 4.2.0)
## Rcpp 1.0.9 2022-07-08 [1] CRAN (R 4.1.2)
## remotes 2.4.2 2021-11-30 [1] CRAN (R 4.1.2)
## reticulate 1.26 2022-08-31 [1] CRAN (R 4.1.2)
## rlang 1.1.1 2023-04-28 [1] CRAN (R 4.1.2)
## rmarkdown 2.23 2023-07-01 [3] CRAN (R 4.3.1)
## rstudioapi 0.15.0 2023-07-07 [3] CRAN (R 4.3.1)
## sass 0.4.7 2023-07-15 [3] CRAN (R 4.3.1)
## sessioninfo 1.2.2 2021-12-06 [1] CRAN (R 4.1.2)
## shiny 1.7.2 2022-07-19 [1] CRAN (R 4.1.2)
## stringi 1.7.12 2023-01-11 [3] CRAN (R 4.2.2)
## stringr 1.5.0 2022-12-02 [1] CRAN (R 4.1.2)
## tibble 3.2.1 2023-03-20 [3] CRAN (R 4.3.1)
## tidyselect 1.2.0 2022-10-10 [3] CRAN (R 4.2.1)
## urlchecker 1.0.1 2021-11-30 [1] CRAN (R 4.1.2)
## usethis 2.1.6 2022-05-25 [1] CRAN (R 4.1.2)
## utf8 1.2.3 2023-01-31 [3] CRAN (R 4.2.2)
## vctrs 0.6.3 2023-06-14 [1] CRAN (R 4.1.2)
## xfun 0.39 2023-04-20 [3] CRAN (R 4.3.0)
## xtable 1.8-4 2019-04-21 [1] CRAN (R 4.1.2)
## yaml 2.3.7 2023-01-23 [3] CRAN (R 4.2.2)
##
## [1] /home/jono/R/x86_64-pc-linux-gnu-library/4.1
## [2] /usr/local/lib/R/site-library
## [3] /usr/lib/R/site-library
## [4] /usr/lib/R/library
##
## ──────────────────────────────────────────────────────────────────────────────